写在前面

秋招告一段落，我也陷入了一阵迷茫期，趁此时间读一些“大学不读以后就永远不会读”的书。与CSAPP齐名的SICP映入眼帘。仍记得大二下学期读CSAPP带给我痛并快乐的经验，也希望SICP同样带给我一些独特的经历和体会。

SICP描述的核心问题是什么？

此文成形之前我只读了第一章（挖坑待填），不是妄加评判，只是读一本经典之前不知道为什么要读等于白读。先说说个人读完第一章的看法，那就是scheme的括号好多。然而读这本书如果陷入语言定义的话就落入下乘了。SICP绝不是一本讲述Lisp编程规范的书，而是用Lisp这种语言从编程世界中最基本的要素出发，逐渐引入编程世界的重要概念，所有这些的要素只有一个目的——如何降低构造大型程序的复杂度。控制复杂度的能力，是区分程序员能力的最重要指标之一，而这本书就是教会你一套控制系统复杂度的方法论和理论体系。scheme这种形而下学的语言反而够用就好，所以本书不会涉及太多语言使用上的讲解。另外熟悉了scheme这种语言的话，括号看起来也有一种独特的美感。

第一章：构造过程抽象（Building Abstractions with Procedures）

We are about to study the idea of a computational process. Computational processes are abstract beings that inhabit computers. As they evolve, processes manipulate other abstract things called data. The evolution of a process is directed by a pattern of rules called a program. People create programs to direct processes. In effect, we conjure the spirits of the computer with our spells.

我们正在学习的是computational process的思想，这也是SICP通篇所讲的内容：编程思想，或者说一个良好运行的复杂系统是如何通过computational process组织起来的。程序并不神秘：**它依附于计算机，通过抽象的过程操控抽象的数据并在程序规范的指导下完成某种智力活动。**程序员有组织程序的能力去执行任务，这种能力包括不限于预见系统行为、构造系统、设想并预防一定的系统问题、系统bug时调试、程序高度的模块化。

Why is Lisp？

程序需要编程语言表达，那为什么是Lisp？

If Lisp is not a mainstream language, why are we using it as the framework for our discussion of programming? Because the language possesses unique features that make it an excellent medium for studying important programming constructs and data structures and for relating them to the linguistic features that support them. The most significant of these features is the fact that Lisp descriptions of processes, called procedures, can themselves be represented and manipulated as Lisp data. The importance of this is that there are powerful program-design techniques that rely on the ability to blur the traditional distinction between "passive" data and “active” processes. As we shall discover, Lisp’s flexibility in handling procedures as data makes it one of the most convenient languages in existence for exploring these techniques. The ability to represent procedures as data also makes Lisp an excellent language for writing programs that must manipulate other programs as data, such as the interpreters and compilers that support computer languages. Above and beyond these considerations, programming in Lisp is great fun.

如果Lisp不是主流语言，为什么我们要用它作为讨论编程的框架？（挖坑待填）主要是因为这种语言具有独特的特性，这使得Lisp本身非常容易研究编程结构和数据结构。这些特性中最重要的是Lisp的过程本身可以作为Lisp数据来表示和操作。

一言以蔽之，Lisp拥有非常灵活的特性，这种特性在研究一些技术的时候必不可少，另外Lisp也可以作为解释器和编译器去执行另一段程序，在第四章和第五章将会看到。

1.1 The Elements of Programming

有很多强有力的编程语言可以帮助我们将思想映射在程序中，可以将它们看作一个一个框架，这样子我们只需要关心如何利用“框架”组合一个复杂系统。每一种语言都提供了三种基本机制：

1. 基本表达式形式
2. 组合机制
3. 抽象机制

当我们学习一门新语言的时候，更加需要注意这三方面。scheme简单但也提供了这样完整的机制。

本小节依次讲解了scheme以下的知识：

• 表达式和组合式、命名和环境
• 组合式的求值
• 过程的定义、复合过程
• 复合过程求值的代换模型
• 条件表达式和谓词
• 将过程作为黑箱的抽象

如果是cs新手，本小节就是教你怎样用符号（scheme语言）映射自己的想法（现实）到一个具体的过程（抽象）。对于老鸟来说，没接触过函数式编程的可以感受一下scheme，顺带巩固一下基础。另外这里其实是有一些重要的东西的。

1. 解释器会响应表达式的求值结果，“过程”可以将表达式组合起来形成复合表达式即组合式。

2. 解释器十分依赖环境保存的内容。没有环境的表达式对解释器是无意义的。

3. 解释器求解组合式只需两步：

   1. 求组合式中各个子表达式的值
   2. 将子表达式的值作为参数应用于最外层的过程

   这一个求值过程明显是递归的。反复应用过程1，最后一定会到达某个点，在这里遇到的不是组合式而是基本表达式，最后可以得到整个组合式的值。

4. 由3.可得一个应用于复合过程的代换模型。

5. 代换模型并不是解释器实际工作方式的具体描述，这只是为了帮助直观理解过程应用的行为的初步模型，比如该模型无法解决“变化的数据”的问题。

最后再来聊一下“语法糖衣”，语言中一些特殊的表达形式/语法被称为语法糖，这种语法对语言的功能并没有影响，也不会影响性能，但是更方便程序员使用，Alan Perlis认为“语法糖会导致分号的癌症”，因为语法糖会导致程序代码缺乏统一性。关于语法糖的优与劣不讨论。Lisp本身极其灵活也有极强的表达性，所以语法糖很少，看起来也更简洁直接。

到了做题时间了，这里有一个牛顿法求平方根的例子，算是一个比较典型的例子了，还有一个斐波那契数列更典型，后续也会有的😀。这里的例题只是为了说明数学上的定义和具体的编程抽象之间的鸿沟。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

;牛顿法求平方根 使用了块结构，未使用lambda
(define (sqrt x)
  (define (improve guess x)
    (< (/ (+ guess x) 2) enough))
  (define enough 0.000001)
  (define (enough-good? guess x)
    (< (- (square guess) x) enough))
  (define (sqrt-iter guess x )
    (if (enough-good? guess x)
         guess
         (sqrt-iter (improve guess x)
                    x)))

书上这道题本意是为了加深对“过程”这一抽象的理解。另外还有挺多有意思的地方，比如这道题明显是一个迭代结构，if的else语句中却是一个递归调用，之后的尾递归会阐述这个过程（挖坑待填），这里也可以想想递归和迭代的效率问题。

1.2 Procedures and the Processes They Generate

上一节仅仅讲了scheme的基本用法，我们可能会试着用“积木”搭建可供运行的程序。然而除了可用之外，对于程序员来说更重要的一点就是预测程序的结果，这个结果不仅仅是完成功能的意思，它包含了性能分析和资源消耗分析。这一节主要分析如何对一个计算过程做出一个整体的行为论断。当然了只是一些数学方法的映射，虽无太大实际意义，但足以让人感受到数学在编程中的美了。

先来看两种递归过程的两种模型

1. 线性递归过程
2. 树形递归过程

阶乘n！的递归计算是一个典型的线性递归过程，上代码

1
2
3
4
5

;①
(define (factorial n)
  (if (= n 1)
      1
      (* n (factorial (- n 1)))))

整个过程展开：

再来看另一种迭代过程

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

;②
(define (factorial n)
  (fact-iter 1 1 n))

(define (fact-iter product counter max-count)
  (if (> counter max-count)
      product
      (fact-iter (* counter product);虽然是自己调用自己，但其描述的是迭代过程
                 (+ counter 1)
                 max-count)))

展开：

通过比较①②过程的展开图，发现①是先展开再收缩的过程，展开阶段构造了一个推迟进行的操作形成的链条，收缩阶段表现为展开链条的实际执行，这就是一个递归计算过程，递归链条是需要被保存的信息量。这也是递归一个比较明确的定义。再观察具体的递归形状，我们会发现递归链条随n值线性增长，这样的递归过程被称为线性递归过程。递归过程的代码表现就是过程自己调用自己。

而②没有任何展开收缩，每一步都在执行具体的计算，这种过程称为迭代计算过程。其状态可以用固定的状态描述，注意我们需要保存每一步的状态值，状态更新的方法，结束迭代的方法。该过程是一个线性迭代的过程。可以看到②也存在自己调用自己的递归形式，然而它仍然是迭代计算过程，这就是scheme里的尾递归。

再从另一个角度来谈谈递归和迭代的不同。递归为了能继续计算下去需要维护整个链条的信息量，这些信息并没有保存在我们定义的变量中（事实上我们也并没有定义变量），而是由解释器维护了这些信息，链条越长需要保存的信息越多，在许多高级语言里面这是由堆栈保存的，如果链条过长就会引发经典错误"Stack over flow"。迭代过程只需要向解释器提供具体数量的变量即可完成整个计算过程，这些变量被放在寄存器中。在C、C++、Java里，对于任何递归过程的解释永远是，所需要消耗的存储量总是与过程调用的数目成正比（堆栈保存链条），即使这一计算过程描述上是迭代的。通俗点说，只要过程调用了自己就一定是递归计算而非迭代计算。这些高级语言为了抽象出迭代过程，不得不借助特殊的语法糖“循环结构”。对于scheme来说，即使是过程自己调用自己（递归过程），也可以在常量空间中执行迭代型计算过程，这一特性的实现被称为尾递归。

Java8不支持尾递归优化，用尾递归语法糖写迭代大概率会爆栈，所以该写迭代还是老老实实写迭代吧😀。

再来看另外一种递归计算：树形递归。最典型的就是斐波那契函数了。

1
2
3
4
5

(define (fib n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1))
                 (fib (- n 2))))))

展开：

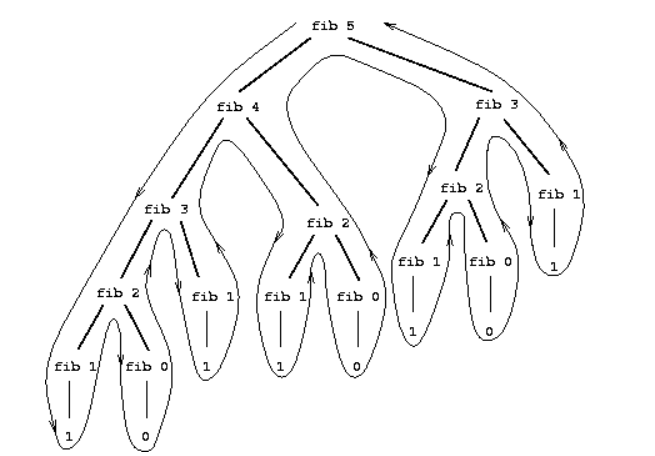
为什么同样是递归计算，fib就产生了一个树形结构呢？这是因为为了计算一个值fib n ，同时调用了两次自己fib (n - 1)、fib (n - 2)。每层有两个分岔即反映了这一点。学过算法的都知道这个结构有太多的冗余计算了，SICP给了一个具体分析冗余多少fib 1 、fib 0的数学方法看看就好。改进的思路就是使用迭代计算改进：用变量保存计算的中间值，使用迭代（尾递归）减少重复计算。最终是一个线性的迭代过程。

然而树形结构并不是一无是处，尤其是在处理天然的树形结构数据的过程中。

做题时间到，这里有个很有趣的题找零钱，看似像背包却又不太像，回头再复习一下背包（挖坑）。抽象一下题目：将总数为a的现金换成n种硬币，问有多少种不同换法？递归计算很容易理解，难点在于如何通过尾递归做到迭代的解法？为什么这个树形递归计算相对于线性递归计算更难找到迭代计算过程？思考ing……

因为只有6种类型的硬币的值，我们可以将cc分成6个独立的函数，每个函数对应一种硬币类型(包括0表示none，只是为了更加明确)。这可以用来将第二次递归调用(- kind -of-coins 1)转换为普通函数调用。然后只剩下第一个递归调用，可以使用累加器进行迭代。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

 (define (count-change-iter amount)
	(cc-fifties amount 0))

 (define (cc-fifties amount acc)
	(cond ((= amount 0) (+ 1 acc))
	 ((< amount 0) acc)
	 (else (cc-fifties (- amount 50)
				(cc-quarters amount acc)))))

 (define (cc-quarters amount acc)
	(cond ((= amount 0) (+ 1 acc))
	 ((< amount 0) acc)
	 (else (cc-quarters (- amount 25)
			 (cc-dimes amount acc)))))

 (define (cc-dimes amount acc)
	(cond ((= amount 0) (+ 1 acc))
	 ((< amount 0) acc)
	 (else (cc-dimes (- amount 10)
			 (cc-nickels amount acc)))))

 (define (cc-nickels amount acc)
	(cond ((= amount 0) (+ 1 acc))
	 ((< amount 0) acc)
	 (else (cc-nickels (- amount 5)
				(cc-pennies amount acc)))))

 (define (cc-pennies amount acc)
	(cond ((= amount 0) (+ 1 acc))
	 ((< amount 0) acc)
	 (else (cc-pennies (- amount 1)
				(cc-nothing amount acc)))))

 (define (cc-nothing amount acc)
	acc)

最后说一句，像这样的树形递归有过多的冗余计算的话，通常我们都是通过dp和备忘录方式来优化的。

最后一个问题，是如何粗略的度量过程对资源的消耗。文中提出的方法是增长的阶，具体概念不重要，重要的是知道这个是表示算法的时间复杂度的就好了。这里有几道很有意思的题可以看一下。当然不要纠结于算法的具体实现，要理解的是我们怎么通过分析去优化了一个过程，这种不断去分析优化代码的严谨和高标准应该伴随我们的职业生涯。

1. 求幂
2. 最大公约数
3. 素数检查

求幂里有一个优化的思想（练习1.16、1.17）：定义一个不变量，要求它在状态之间保持不变，从而找到迭代的优化方向。这一算法思想叫做“俄罗斯农民的方法”，还是挺有意思的。

1
2
3
4
5
6
7
8

(define (fast-expt-iter p n a)
  (cond
    ((= n 0) a)
    ((even? n) (fast-expt-iter (* p p) (/ n 2) a))
    (else (fast-expt-iter p (- n 1) (* a p)))))

(define (fast-expt2 p n)
  (fast-expt-iter p n 1))

最大公约数也描述了一个简单的算法思想来优化代码的复杂度，叫做“欧几里得算法”。

同样的，素数检查里也介绍了“费马检测”去优化猜测的过程。这里需要注意的地方是这个算法并不能保证完完全全的验正一个数是否是素数，这样的算法叫做概率算法。费马检测也是RSA算法的基础，有时间再去看一看RSA是怎么实现的。腾讯二面面试官问过这个问题😀。

1.3 Formulating Abstractions with Higher-Order Procedures

Higher-Order Procedures即高阶函数。对于熟悉了面对对象编程语言的人来说，好像没有太多的接触过高阶函数这个概念，个人认为这是编程范式不同导致的。对于OOP来说，类就是一等公民，世间万物全部都可以抽象成类，然而在FP中没有对象的概念，函数就是一等公民。高阶函数说简单点就是函数可作为另一个函数的参数，函数也可以作为函数的返回值。官方定义：高阶函数是至少满足下列一个条件的函数：

• 接受一个或多个函数作为输入
• 输出一个函数

这一节可以说是重中之重了，主要讲了高阶函数作为一种抽象机制，如何提高了语言的表达能力。具体来说，过程的抽象使得我们不用对一些过程的细节重复实现而可以直接调用过程完成我们的工作。一些过程可能共享着一套公共模式，将这种模式抽象出来，实现为高阶函数可以来表述计算的一般性过程。我们观察到了有些计算过程有很多重复的模式，于是提出了 “提取公共模式” 这种思想，这也是设计模式里面模板方法的根本理论基础。

这里有几个例子，代码写的非常精彩，会让人惊叹代码还能这么玩！

1. 区间折半查找方程的根
2. 找出函数的不动点
3. 牛顿法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

;区间折半查找方程的根,过程f作为参数
(define (search f neg-point pos-point)
  (let ((midpoint (average neg-point pos-point)))
    (if (close-enough? neg-point pos-point)
        midpoint
        (let ((test-value (f midpoint)))
          (cond ((positive? test-value)
                 (search f neg-point midpoint))
                ((negative? test-value)
                 (search f midpoint pos-point))
                (else midpoint))))))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

;找出函数的不动点
(define tolerance 0.00001)
(define (fixed-point f first-guess)
  (define (close-enough? v1 v2)
    (< (abs (- v1 v2)) tolerance))
  (define (try guess)
    (let ((next (f guess)))
      (if (close-enough? guess next)
          next
          (try next))))
  (try first-guess))

1
2
3
4
5
6

;牛顿法
(define (newton-transform g)
  (lambda (x)
    (- x (/ (g x) ((deriv g) x)))))
(define (newtons-method g guess)
  (fixed-point (newton-transform g) guess))

最后的抽象。因为牛顿法本质上也利用了不动点，所以我们可以抽象出来一个高阶过程：

1
2

(define (fixed-point-of-transform g transform guess)
  (fixed-point (transform g) guess))

这个非常具有一般性（高度抽象）的过程有一个计算某个函数的过程参数g，一个变换g的过程transform，一个初始猜测，就可以返回一个变换g的不动点。

Summury

• 尾递归
• lambda
• 高阶函数